ما هو التفرطح؟
التفرطح هو مقياس إحصائي يستخدم لوصف خاصية مجموعة البيانات. عندما يتم رسم البيانات الموزعة بشكل طبيعي على رسم بياني، فإنها تأخذ شكل جرس مقلوب. وهذا ما يسمى بمنحنى الجرس. عادةً ما تشكل البيانات المخططة الأبعد عن متوسط البيانات ذيول على كل جانب من جوانب المنحنى. يشير التفرطح إلى مقدار البيانات الموجودة في الذيول.
تحتوي التوزيعات ذات التفرطح الكبير على بيانات ذيل أكثر من البيانات الموزعة بشكل طبيعي، والتي يبدو أنها تجلب الذيل نحو الوسط. تحتوي التوزيعات ذات التفرطح المنخفض على عدد أقل من بيانات الذيل، والتي يبدو أنها تدفع ذيول منحنى الجرس بعيدًا عن الوسط.
بالنسبة للمستثمرين، يشير التفرطح العالي لتوزيع العوائد إلى أن المستثمر سيواجه عوائد قصوى عرضية (سواء كانت إيجابية أو سلبية)، أكثر تطرفًا من + أو – ثلاثة انحرافات معيارية عن المتوسط الذي يتوقعه التوزيع الطبيعي للعائدات. تُعرف هذه الظاهرة بخطر التفرطح.
ملخص لأهم النقاط
- يصف التفرطح “سمنة” الذيول الموجودة في التوزيعات الاحتمالية.
- هناك ثلاث فئات من التفرطح هي: ميزوكورتيك (طبيعي) وبلاتيكورتيك (أقل من الطبيعي) و ليبتوكورتيك (أكثر من الطبيعي).
- تعتبر مخاطر التفرطح قياسًا لعدد المرات التي يتحرك فيها سعر الاستثمار بشكل كبير.
- تخبرك خاصية التفرطح في المنحنى بمقدار مخاطر التفرطح في الاستثمار الذي تقيمه.
تحليل التفرطح
التفرطح هو مقياس للوزن المجمع لذيول التوزيع بالنسبة لمركز التوزيع. عندما يتم رسم مجموعة من البيانات العادية تقريبًا عبر رسم بياني، فإنها تُظهر ذروة الجرس ومعظم البيانات ضمن + أو – ثلاثة انحرافات معيارية للمتوسط. ومع ذلك، عند وجود التفرطح العالي، تمتد ذيولها أبعد من + أو – ثلاثة انحرافات معيارية للتوزيع الطبيعي لمنحنى الجرس.
أحيانًا يتم الخلط بين التفرطح وقياس ذروة التوزيع. ومع ذلك، فإن التفرطح هو مقياس يصف شكل ذيول التوزيع بالنسبة لشكله العام. يمكن أن يصل التوزيع إلى ذروته بلا حدود من خلال التفرطح المنخفض، ويمكن أن يكون التوزيع مسطحًا تمامًا مع التفرطح اللانهائي. وبالتالي، يقيس التفرطح “الذيل” وليس “الذروة”.
حساب التفرطح
حساب مع جداول البيانات
هناك عدة طرق مختلفة لحساب التفرطح. إن أبسط طريقة هي استخدام صيغة إكسل Excel أو غوغل شيتس Google Sheets. على سبيل المثال، افترض أن لديك البيانات النموذجية التالية: 4 و5 و6 و3 و4 و5 و6 و7 و5 و8 موزعة في الخلايا من A1 إلى A10 في جدول البيانات. تستخدم جداول البيانات هذه الصيغة لحساب التفرطح: 1
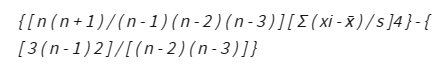 ومع ذلك، سنستخدم الصيغة التالية في جداول بيانات غوغل، والتي تحسبها لنا، على افتراض أن البيانات موجودة في الخلايا من A1 إلى A102:
ومع ذلك، سنستخدم الصيغة التالية في جداول بيانات غوغل، والتي تحسبها لنا، على افتراض أن البيانات موجودة في الخلايا من A1 إلى A102:
التفرطح = (A1: A10)
والنتيجة هي تفرطح بمقدار -0.1518 ، مما يشير إلى أن المنحنى له ذيول أفتح ويكون مسطحًا.
حساب باليد
يعد حساب التفرطح باليد مسعى طويلاً، ويستغرق عدة خطوات للوصول إلى النتائج. سنستخدم نقاط بيانات جديدة ونحد من عددها لتبسيط العملية الحسابية. نقاط البيانات الجديدة هي 27 و13 و17 و57 و113 و25.
من المهم ملاحظة أن حجم العينة يجب أن يكون أكبر بكثير من هذا؛ نستخدم ستة أرقام لتقليل خطوات الحساب. القاعدة الأساسية الجيدة هي استخدام 30% من بياناتك للمجموعات السكانية الأقل من 1000. بالنسبة للسكان الأكبر، يمكنك استخدام 10%.3
أولا، تحتاج إلى حساب المتوسط. اجمع الأرقام واقسم على ستة لتحصل على 42. بعد ذلك، استخدم المعادلات التالية لحساب مجموعين، s2 (مربع الانحراف عن الوسط) وs4 (مربع الانحراف عن المربع المتوسط). ملاحظة: هذه الأرقام لا تمثل الانحراف المعياري، ولكنها تمثل تباين كل نقطة بيانات.45
- s2 = Σ ( yi – ȳ )2
- s4 = Σ ( yi – ȳ )4
حيث:
- yi = المتغير ith للعينة
- ȳ = المتوسط
للحصول على s2، استخدم كل متغير، اطرح المتوسط، ثم قم بتربيع النتيجة. اجمع كل النتائج معًا:
- (27 – 42)2 = (-15)2 = 225
- (13 – 42)2 = (-29)2 = 841
- (17 – 42)2 = (-25)2 = 625
- (57 – 42)2 = (15)2 = 225
- (113 – 42)2 = (71)2 = 5041
- (25 – 42)2 = (-17)2 = 289
- 225 + 841 + 625+ 225 + 5,041 + 289 = 7,246
للحصول على s4، استخدم كل متغير، اطرح المتوسط، وارفع الناتج إلى الأس الرابع. اجمع كل النتائج معًا:
- (27 – 42)4 = (-15)4 = 50,625
- (13 – 42)4 = (-29)4 = 707,281
- (17 – 42)4 = (-25)4 = 390,625
- (57 – 42)4 = (15)4 = 50,625
- (113 – 42)4 = (71)4 = 25,411,681
- (25 – 42)4 = (-17)4 = 83,521
- 50,625+707,281+390,625+50,625+25,411,681+83,521 = 26,694,358
إذن، المجموعان هما:
- s2 = 7,246
- s4 = 26,694,358
الآن، احسب m2 وm4، اللحظات الثانية والرابعة من صيغة التفرطح:
- m2 = s2 / n, or 7,246 / 6 = 1,207.67
- m4 = s4 / n, or 26,694,358 / 6 = 4,449,059.67
يمكننا الآن حساب التفرطح باستخدام صيغة موجودة في العديد من كتب الإحصاء المدرسية التي تفترض التوزيع الطبيعي تمامًا مع تفرطح صفري:
![]()
حيث:
- k = التفرطح
- m4 = اللحظة الرابعة
- m2 = اللحظة الثانية
- 4,449,059.67 / 1,458,466.83 = 3.05
إذن، التفرطح لمتغيرات العينة هو 3.05 – 3، أو 0.05.
أنواع التفرطح
توجد ثلاث فئات من التفرطح يمكن عرضها بواسطة مجموعة من البيانات. تتم مقارنة جميع مقاييس التفرطح مع التوزيع الطبيعي القياسي أو منحنى الجرس.
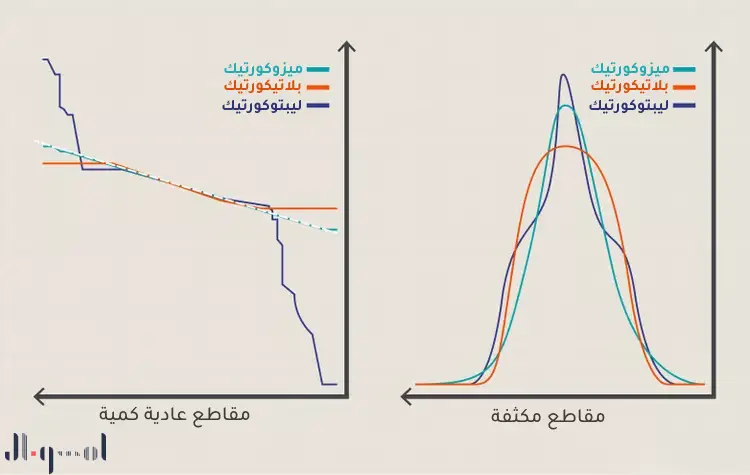
الفئة الأولى (التفرطح = 3.0) هي توزيع مسوكورتي. يحتوي هذا التوزيع على إحصاء تفرطح مشابه للتوزيع الطبيعي، مما يعني أن خاصية القيمة القصوى للتوزيع مشابهة للتوزيع الطبيعي.
الفئة الثانية (التفرطح > 3.0) هي توزيع ليبتوكورتيك. أي توزيع يكون ليبتوكورتيك يعرض تفرطحًا أكبر من التوزيع ميسوكورتيك. خصائص هذا التوزيع ذات ذيول طويلة (قيم متطرفة). بادئة “lepto-” تعني “نحيف”، مما يجعل شكل التوزيع ليبتوكورتيك أسهل في التذكر. إن “النحافة” لتوزيع ليبتوكورتيك هي نتيجة للقيم المتطرفة، والتي تمد المحور الأفقي للرسم البياني، مما يجعل الجزء الأكبر من البيانات يظهر في نطاق رأسي ضيق (“نحيف”). وهكذا توصف أحيانًا التوزيعات اللبتوكورتية بأنها “مركزة نحو المتوسط”، ولكن القضية الأكثر صلة (خاصة بالنسبة للمستثمرين) هي وجود قيم متطرفة عرضية تسبب ظهور هذا “التركيز”. أمثلة التوزيعات ليبتوكورتيك هي توزيعات T بدرجات صغيرة من الحرية.
الفئة الأخيرة (التفرطح < 3.0) هي توزيع بلاتيكورتيك. هذا الأنواع من التوزيعات لها ذيول قصيرة (ندرة القيم المتطرفة). وتعني بادئة “بلاتي” “واسع”، والمقصود منها وصف ذروة قصيرة وواسعة المظهر، لكن هذا خطأ تاريخي. التوزيعات المنتظمة هي بلاتيكورتيك ولها قمم واسعة، ولكن توزيع بيتا (.5،1) هو أيضًا بلاتيكورتي وله ذروة مدببة بلا حدود. السبب في أن هذين التوزيعين هما بلاتيكورتيك هو أن قيمهما القصوى أقل من التوزيع الطبيعي. بالنسبة للمستثمرين، تكون توزيعات العوائد المستقرة ثابتة ويمكن التنبؤ بها، بمعنى أنه نادرًا ما تكون هناك عوائد (متطرفة) (إن وجدت).
استخدام التفرطح
يستخدم التفرطح في التحليل المالي لقياس مخاطر الاستثمار في تقلب الأسعار. يختلف خطر التفرطح عن القياسات الأكثر شيوعًا مثل ألفا أو بيتا أو آر تربيع أو نسبة شارب. يقيس ألفا العائد الزائد بالنسبة لمؤشر مرجعي، ويقيس بيتا التقلب الذي يقارن السهم بالسوق الأوسع.
يقيس آر تربيع R-squared النسبة المئوية للحركة التي تمتلكها المحفظة أو الصندوق والتي يمكن تفسيرها من خلال معيار، وتقارن نسبة شارب Sharpe العائد إلى المخاطر. يقيس التفرطح مقدار التقلبات التي يشهدها سعر الاستثمار بانتظام.
على سبيل المثال، تخيل أن متوسط سعر السهم 25.85 دولارًا لكل سهم. إذا تأرجح سعر السهم على نطاق واسع ومتكرر بشكل كافي، فسيكون لمنحنى الجرس ذيول ثقيلة (التفرطح العالي). هذا يعني أن هناك الكثير من التباين في سعر السهم – يجب على المستثمر أن يتوقع تقلبات كبيرة في الأسعار في كثير من الأحيان.
إذا كان للسهم ذيول خفيفة (تفرطح منخفض)، فقد يتوقع المستثمر أن يتأرجح سعر السهم على نطاق واسع فقط من حين لآخر.
أسئلة شائعة
لماذا التفرطح مهم؟
يشرح التفرطح عدد المرات التي تقع فيها الملاحظات في بعض مجموعات البيانات في الذيول مقابل مركز التوزيع الاحتمالي. في التمويل والاستثمار، يتم تفسير التفرطح الزائد على أنه نوع من المخاطر يُعرف باسم “مخاطر الذيل”، أو فرصة حدوث خسارة بسبب حدث نادر، كما هو متوقع من قبل توزيع الاحتمالات. إذا كانت مثل هذه الأحداث أكثر شيوعًا مما يتوقعه التوزيع، يُقال إن ذيولها “سمينة”.
ما هو التفرطح الزائد؟
يقارن التفرطح الزائد معامل التفرطح مع معامل التوزيع الطبيعي. يُفترض أن تحتوي معظم التوزيعات الطبيعية على تفرطح من ثلاثة، لذلك سيكون التفرطح الزائد أكثر أو أقل من ثلاثة؛ ومع ذلك، تفترض بعض النماذج أن التوزيع الطبيعي له تفرطح صفري، لذا فإن التفرطح الزائد سيكون أكثر أو أقل من الصفر.
هل التفرطح هو نفسه الانحراف؟
لا. يقيس التفرطح مقدار البيانات في توزيع الاحتمالية التي تتمحور حول الوسط (الوسط) مقابل الذيول. يقيس الانحراف بدلاً من ذلك التناظر النسبي للتوزيع حول المتوسط.
الخلاصة
يصف التفرطح مقدار التوزيع الاحتمالي الذي يقع في ذيل بدلاً من المركز. في التوزيع الطبيعي، يساوي التفرطح ثلاثة (أو صفر في بعض النماذج). سيؤدي التفرطح الزائد الإيجابي أو السلبي إلى تغيير شكل التوزيع وفقًا لذلك. بالنسبة للمستثمرين، يعد التفرطح مهمًا في فهم مخاطر الذيل أو مدى تكرار الأحداث “غير المعتادة”، نظرًا لافتراض المرء حول توزيع عوائد الأسعار.
تمت الترجمة عن موقع انفستوبيديا
هوامش
- https://support.microsoft.com/en-us/office/kurt-function-bc3a265c-5da4-4dcb-b7fd-c237789095ab
- https://support.google.com/docs/answer/3093634?hl=en
- https://wp.stolaf.edu/iea/sample-size/
- https://www150.statcan.gc.ca/n1/edu/power-pouvoir/ch12/5214891-eng.htm
- https://stats.oarc.ucla.edu/other/mult-pkg/faq/general/faq-whats-with-the-different-formulas-for-kurtosis/
