انحدار (Regression)

ما هو الانحدار (Regression)؟

الانحدار هو طريقة إحصائية تستخدم في التمويل والاستثمار وغيرها من التخصصات التي تحاول تحديد قوة وطبيعة العلاقة بين متغير تابع واحد (يشار إليه عادة بـ ص أو (Y)) وسلسلة من المتغيرات الأخرى (المعروفة باسم المتغيرات المستقلة).
يُسمى أيضًا الانحدار البسيط أو المربعات الصغرى العادية (OLS)، والانحدار الخطي هو الشكل الأكثر شيوعًا لهذه التقنية. ينشئ الانحدار الخطي العلاقة الخطية بين متغيرين بناءً على خط التوافق الأفضل. وبالتالي يتم تصوير الانحدار الخطي بيانيا باستخدام خط مستقيم مع تحديد المنحدر كيف يؤثر التغيير في متغير واحد على التغيير في الآخر. يمثل التقاطع y لعلاقة الانحدار الخطي قيمة أحد المتغيرات عندما تكون قيمة الآخر صفرًا. توجد أيضًا نماذج انحدار غير خطية، ولكنها أكثر تعقيدًا بكثير.
يعد تحليل الانحدار أداة قوية للكشف عن الارتباطات بين المتغيرات التي تمت ملاحظتها في البيانات، ولكن لا يمكن الإشارة بسهولة إلى السببية. يتم استخدامه في العديد من السياقات في الأعمال التجارية والمالية والاقتصاد. ولا ينبغي الخلط بين الانحدار كأسلوب إحصائي ومفهوم الانحدار إلى المتوسط ​​(الارتداد المتوسط).
على سبيل المثال، يتم استخدام الانحدار لمساعدة مديري الاستثمار على تقييم الأصول وفهم العلاقات بين عوامل مثل أسعار السلع الأساسية ومخزونات الشركات التي تتداول تلك السلع.

ملخص لأهم النقاط

• الانحدار هو أسلوب إحصائي يربط المتغير التابع بواحد أو أكثر من المتغيرات المستقلة (التفسيرية).
• نموذج الانحدار قادر على إظهار ما إذا كانت التغييرات الملحوظة في المتغير التابع مرتبطة بالتغيرات في واحد أو أكثر من المتغيرات التوضيحية.
• يقوم بذلك عن طريق ملاءمة الخط الأفضل ورؤية كيفية توزيع البيانات حول هذا الخط.
• يساعد الانحدار الاقتصاديين والمحللين الماليين في أشياء تتراوح من تقييم الأصول إلى وضع التنبؤات.
• لكي يتم تفسير نتائج الانحدار بشكل صحيح، يجب أن تكون هناك عدة افتراضات حول البيانات والنموذج نفسه.

مفهوم الانحدار

يلتقط الانحدار الارتباط بين المتغيرات التي تمت ملاحظتها في مجموعة البيانات ويحدد ما إذا كانت تلك الارتباطات ذات دلالة إحصائية أم لا.
النوعان الأساسيان من الانحدار هما الانحدار الخطي البسيط والانحدار الخطي المتعدد، على الرغم من وجود طرق انحدار غير خطية للبيانات والتحليلات الأكثر تعقيدًا. يستخدم الانحدار الخطي البسيط متغيرًا مستقلاً واحدًا لشرح أو التنبؤ بنتيجة المتغير التابع ص، بينما يستخدم الانحدار الخطي المتعدد متغيرين مستقلين أو أكثر للتنبؤ بالنتيجة (مع الحفاظ على ثبات جميع المتغيرات الأخرى).
يمكن أن يساعد الانحدار المتخصصين في التمويل والاستثمار وكذلك المتخصصين في الشركات الأخرى. يمكن أن يساعد الانحدار أيضًا في التنبؤ بمبيعات الشركة بناءً على الطقس أو المبيعات السابقة أو نمو الناتج المحلي الإجمالي أو أنواع أخرى من الظروف. نموذج تسعير الأصول الرأسمالية (CAPM) هو نموذج انحداري شائع الاستخدام في التمويل لتسعير الأصول واكتشاف تكاليف رأس المال.

الانحدار والاقتصاد القياسي

الاقتصاد القياسي هو مجموعة من التقنيات الإحصائية المستخدمة لتحليل البيانات في التمويل والاقتصاد. مثال على تطبيق الاقتصاد القياسي هو دراسة تأثير الدخل باستخدام بيانات يمكن ملاحظتها. على سبيل المثال، قد يفترض الاقتصادي أنه عندما يزيد الشخص دخله فإن إنفاقه سيزداد أيضًا.
إذا أظهرت البيانات وجود مثل هذا الارتباط، فيمكن بعد ذلك إجراء تحليل الانحدار لفهم قوة العلاقة بين الدخل والاستهلاك وما إذا كانت تلك العلاقة ذات دلالة إحصائية أم لا – أي أنه يبدو من غير المرجح أن تكون كذلك. بسبب الصدفة وحدها.
لاحظ أنه يمكن أن يكون لديك العديد من المتغيرات التوضيحية في تحليلك – على سبيل المثال، التغيرات في الناتج المحلي الإجمالي والتضخم بالإضافة إلى البطالة في تفسير أسعار سوق الأسهم. عند استخدام أكثر من متغير توضيحي، يشار إلى ذلك باسم الانحدار الخطي المتعدد. هذه هي الأداة الأكثر استخدامًا في الاقتصاد القياسي.
يتم انتقاد الاقتصاد القياسي في بعض الأحيان لاعتماده بشكل كبير على تفسير مخرجات الانحدار دون ربطه بالنظرية الاقتصادية أو البحث عن آليات سببية. ومن الأهمية بمكان أن تكون النتائج التي تم الكشف عنها في البيانات قادرة على تفسيرها بشكل مناسب من خلال النظرية، حتى لو كان ذلك يعني تطوير نظريتك الخاصة للعمليات الأساسية.

حساب الانحدار

غالبًا ما تستخدم نماذج الانحدار الخطي أسلوب المربعات الصغرى لتحديد الخط الأفضل. يتم تحديد أسلوب المربعات الصغرى عن طريق تقليل مجموع المربعات التي تم إنشاؤها بواسطة دالة رياضية. ويتم تحديد المربع بدوره من خلال تربيع المسافة بين نقطة البيانات وخط الانحدار أو القيمة المتوسطة لمجموعة البيانات.

بمجرد اكتمال هذه العملية (عادة ما تتم اليوم باستخدام البرمجيات)، يتم إنشاء نموذج الانحدار. الشكل العام لكل نوع من نماذج الانحدار هو:

الانحدار الخطي البسيط:¹

Y = a + bX + u

الانحدار الخطي المتعدد:²

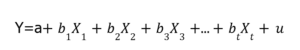
حيث:

Y = المتغير التابع الذي تحاول التنبؤ به أو شرحه

X = المتغير (المتغيرات) التوضيحية (المستقلة) التي تستخدمها للتنبؤ أو الارتباط ب Y

a = تقاطع y

b = (معامل بيتا) هو ميل المتغير (المتغيرات) التفسيرية

u = مصطلح الانحدار المتبقي أو الخطأ

مثال على كيفية استخدام تحليل الانحدار في التمويل

غالبًا ما يستخدم الانحدار لتحديد عدد العوامل المحددة مثل سعر السلعة أو أسعار الفائدة أو صناعات أو قطاعات معينة تؤثر على حركة سعر الأصل. ويستند نموذج تسعير الأصول الرأسمالية المذكور أعلاه على الانحدار، ويتم استخدامه لتوقع العوائد المتوقعة للأسهم وتوليد تكاليف رأس المال. تتراجع عوائد السهم مقابل عوائد مؤشر أوسع، مثل مؤشر ستاندرد آند بورز 500 (S&P 500)، لإنشاء مقياس تقلب (بيتا) لسهم معين.
بيتا (Beta) هي مقياس للمخاطر المحيطة بالاستثمار في السهم فيما يتعلق بالسوق أو المؤشر وتنعكس كانحدار في نموذج تسعير الأصول الرأسمالية. سيكون عائد السهم المعني هو المتغير التابع ص، في حين أن المتغير المستقل س سيكون علاوة مخاطر السوق.
يمكن إضافة متغيرات إضافية مثل القيمة السوقية للسهم ونسب التقييم والعوائد الأخيرة إلى نموذج تسعير الأصول الرأسمالية للحصول على تقديرات أفضل للعائدات. تُعرف هذه العوامل الإضافية باسم عوامل فاما فرينش (Fama-French)، والتي سميت على اسم الأساتذة الذين طوروا نموذج الانحدار الخطي المتعدد لتفسير عوائد الأصول بشكل أفضل.³

أسئلة شائعة

لماذا يطلق على الانحدار هذا الاسم؟

على الرغم من وجود بعض الجدل حول أصول الاسم، فإن التقنية الإحصائية الموصوفة أعلاه على الأرجح أطلق عليها اسم “الانحدار” من قبل السير فرانسيس غالتون في القرن التاسع عشر لوصف السمة الإحصائية للبيانات البيولوجية (مثل ارتفاعات الأشخاص في مجتمع ما). للرجوع إلى مستوى متوسط ​​ما. بمعنى آخر، في حين أن هناك أشخاصًا أقصر وأطول، فإن القيم المتطرفة فقط هي التي تكون طويلة جدًا أو قصيرة جدًا، ومعظم الناس يتجمعون في مكان ما حول (أو “يتراجعون” إلى) المتوسط.⁴

ما هو الغرض من الانحدار؟

في التحليل الإحصائي، يتم استخدام الانحدار لتحديد الارتباطات بين المتغيرات التي تحدث في بعض البيانات. ويمكنه إظهار حجم هذا الارتباط وكذلك تحديد أهميته الإحصائية (أي ما إذا كان الارتباط محتملًا بسبب الصدفة أم لا). يعد الانحدار أداة قوية للاستدلال الإحصائي، وقد تم استخدامه أيضًا لمحاولة التنبؤ بالنتائج المستقبلية بناءً على الملاحظات السابقة.

كيف يتم تفسير نموذج الانحدار؟

قد يكون مخرج نموذج الانحدار على الشكل التالي: Y = 1.0 + (3.2)X1 – 2.0(X2) + 0.21.

لدينا هنا انحدار خطي متعدد يربط بعض المتغيرات (Y) مع متغيرين توضيحيين (X1) و(X2). سوف نفسر النموذج على أن قيمة (Y) تتغير بمقدار 3.2 مرة لكل تغيير في وحدة واحدة في (X1) (إذا ارتفع (X1) بمقدار 2، وارتفع (Y) بمقدار 6.4، وما إلى ذلك) مع الحفاظ على ثبات كل شيء آخر (جميع الأشياء الأخرى متساوية). وهذا يعني التحكم في (X2)، (X1) لديه هذه العلاقة الملحوظة. وبالمثل، مع الحفاظ على (X1) ثابتًا، فإن كل وحدة زيادة في (X2) ترتبط بانخفاض 2x في (Y). يمكننا أيضًا ملاحظة تقاطع (Y) لـ 1.0، مما يعني أن (Y) تساوي 1 عندما يكون (X1) و(X2) كلاهما صفرًا. مصطلح الخطأ (المتبقي) هو 0.21.⁵

ما هي الافتراضات التي يجب أن تصمد لنماذج الانحدار؟

من أجل تفسير مخرجات نموذج الانحدار بشكل صحيح، يجب أن تحمل الافتراضات الرئيسية التالية حول عملية البيانات الأساسية لما تقوم بتحليله:

• العلاقة بين المتغيرات خطية
• التجانس أو أن تباين المتغيرات ومصطلح الخطأ يجب أن يظل ثابتًا
• جميع المتغيرات التفسيرية مستقلة عن بعضها البعض
• يتم توزيع جميع المتغيرات بشكل طبيعي⁶

الخلاصة

‏الانحدار هو طريقة إحصائية تحاول تحديد قوة وطبيعة العلاقة بين متغير تابع واحد وسلسلة من المتغيرات الأخرى. يتم استخدامه في التمويل والاستثمار والتخصصات الأخرى. ‏
يكشف تحليل الانحدار عن الارتباطات بين المتغيرات التي لوحظت في البيانات، ولكن لا يمكنه أن يشير بسهولة إلى السببية.‏

1. Margo Bergman. “Quantitative Analysis for Business: 12. Simple Linear Regression and Correlation.” University of Washington Pressbooks, 2022.
2. Margo Bergman. “Quantitative Analysis for Business: 13. Multiple Linear Regression.” University of Washington Pressbooks, 2022.
3. Fama, Eugene F., and Kenneth R. French, via Wiley Online Library. “The Cross-Section of Expected Stock Returns.” The Journal of Finance, vol. 47, no. 2, June 1992, pp. 427–465.
4. Stanton, Jeffrey M., via Taylor & Francis Online. “Galton, Pearson, and the Peas: A Brief History of Linear Regression for Statistics Instructors.” Journal of Statistics Education, vol. 9, no. 3, 2001.
5. Margo Bergman. “Quantitative Analysis for Business: 13. Multiple Linear Regression.” University of Washington Pressbooks, 2022.
6. CFA Institute. “Basics of Multiple Regression and Underlying Assumptions.”