ما هي الفائدة المركبة؟
الفائدة المركبة هي الفائدة على القرض أو الوديعة محسوبة على أساس كل من المبلغ الأساسي والفائدة المتراكمة من الفترات السابقة. ويُعتقد أن الفائدة المركبة نشأت في إيطاليا في القرن السابع عشر، ويمكن التفكير بها على أنها “فائدة على الفائدة”، وستجعل المجموع يزداد بمعدل أسرع من الفائدة البسيطة، والتي يتم حسابها فقط على المبلغ الأساسي.
يعتمد المعدل الذي تتراكم عنده الفائدة المركبة على تكرار التراكب، بحيث أنه كلما زاد عدد الفترات المركبة، زادت الفائدة المركبة. وبالتالي، فإن مبلغ الفائدة المركبة المتراكمة على 100 دولار مركب عند 10٪ سنويًا سيكون أقل من 100 دولار مركبة بمعدل 5٪ كل نصف سنة خلال نفس الفترة الزمنية. وذلك لأن تأثير الفائدة على الفائدة يمكن أن يولد عوائد إيجابية متزايدة بناءً على المبلغ الأساسي، وتمت الإشارة إلى ذلك أحيانًا على أنه “معجزة الفائدة المركبة”.
ملخص لأهم النقاط:
- الفائدة المركبة هي الفائدة المحسوبة على المبلغ الأساسي، والتي تشمل أيضًا جميع الفوائد المتراكمة من الفترات السابقة على وديعة أو قرض.
- يتم احتساب الفائدة المركبة بضرب المبلغ الأساسي الأولي بواحد مضافًا إلى معدل الفائدة السنوية مرفوعان إلى عدد الفترات المركبة مطروحًا منه واحدًا.
- يمكن مضاعفة الفائدة باستخدام مختلف جداول التكرار الزمنية، من المستمرة إلى اليومية إلى السنوية.
- عند حساب الفائدة المركبة، فإن عدد الفترات المركبة يحدث فرقًا كبيرًا.
حساب الفائدة المركبة
يتم احتساب الفائدة المركبة بضرب المبلغ الأساسي بواحد مضاف إلى معدل الفائدة السنوية ومرفوعان إلى عدد الفترات المركبة ومطروحًا منه واحدًا. ثم يتم طرح المبلغ الأولي الإجمالي للقرض من القيمة الناتجة.
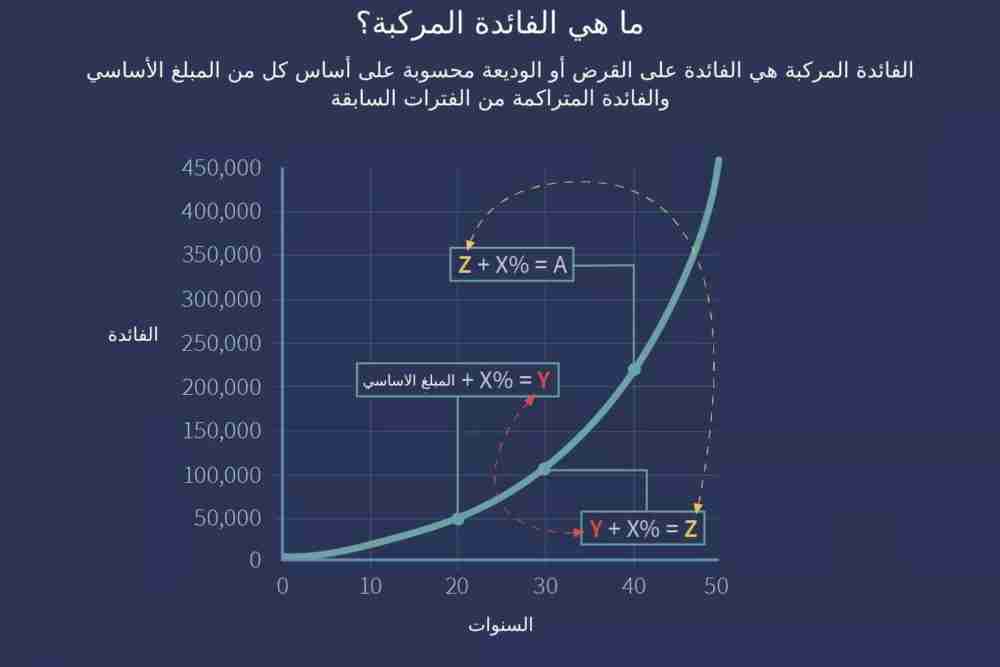
صيغة حساب الفائدة المركبة هي:
الفائدة المركبة = إجمالي المبلغ الأساسي والفائدة في المستقبل (أو القيمة المستقبلية) مطروحًا منه المبلغ الأساسي في الوقت الحالي (أو القيمة الحالية)
= [P (1 + i)n] – P
= P [(1 + i)n – 1]
حيث P = المبلغ الأساسي، i = معدل الفائدة الاسمية السنوي كنسبة مئوية، و n = عدد الفترات المركبة.)
افترض قرض مدته ثلاث سنوات بقيمة 10,000 دولار وبسعر فائدة 5٪ مركب سنويًا. ما هو مقدار الفائدة؟ في هذه الحالة، سيكون:
$10,0001+0.053-1=$10,0001.157625-1=$1,576.25
نمو الفائدة المركبة
باستخدام المثال أعلاه، نظرًا لأن الفائدة المركبة تأخذ أيضًا في الاعتبار الفائدة المتراكمة في الفترات السابقة، فإن مبلغ الفائدة لا يتساوى لجميع السنوات الثلاث، كما سيكون في حالة استخدام الفائدة بسيطة. في حين أن إجمالي الفائدة المستحقة الدفع خلال فترة الثلاث سنوات لهذا القرض هو 1,576.25 دولارًا أمريكيًا، فإن الفائدة مستحقة الدفع في نهاية كل عام موضحة في الرسم البياني أدناه.
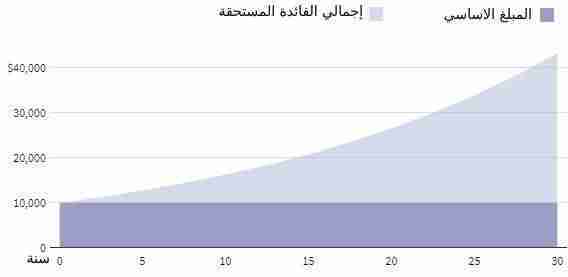
كيف تنمو الفائدة المركبة بمرور الوقت
لو استثمرت 10,000 دولار بفائدة مركبة سنوية 5% ستكون قيمته 40,000 دولار بعد 30 سنة، مراكمًا فائدة بقيمة 30,000 دولار.
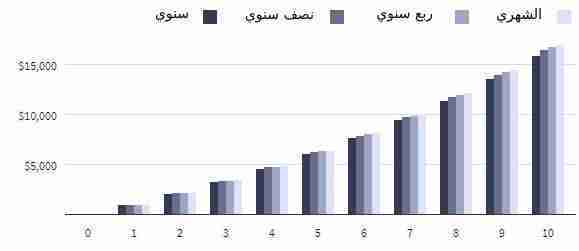
تأثير الفترات المركبة
تعني فترات التركيب الأكثر تواترًا فائدة مركبة أكبر، لكن التردد له عوائد متناقصة. يوضح هذا المثال الفائدة المتراكمة على قرض بقيمة 10000 دولار أمريكي والذي يتراكم سنويًا بنسبة 10٪ لأربع فترات مركبة مختلفة على مدى 10 سنوات.
يمكن أن تزيد الفائدة المركبة بشكل كبير من عوائد الاستثمار على المدى الطويل. في حين أن إيداع 100.000 دولار الذي يتلقى فائدة سنوية بسيطة بنسبة 5٪ سيكسب 50،000 دولار من الفائدة الإجمالية على مدى 10 سنوات، فإن الفائدة المركبة السنوية بنسبة 5٪ على 10.000 دولار ستصل إلى 62.889,46 دولارًا أمريكيًا خلال نفس الفترة. إذا تم بدلاً من ذلك دفع فترة التراكم شهريًا خلال نفس فترة العشر سنوات بفائدة مركبة بنسبة 5٪، فإن إجمالي الفائدة سينمو بدلاً من ذلك إلى 64700.95 دولارًا.1
حساب الفائدة المركبة باستخدام اكسل (Excel)
لا داعي للقلق اذا كنت تشعر بأنه قد عفا الزمن على ما تعلمته في دروس الرياضيات فهناك العديد من الأدوات المفيدة للمساعدة في تحديد التركيب. العديد من الآلات الحاسبة (سواء المحمولة أو المعتمدة على الكمبيوتر) التي تحتوي على دالة الأس التي يمكن استخدامها لهذه الأغراض. وإذا ظهرت مسائل تركيب أكثر تعقيدًا، فيمكن إجراؤها باستخدام Microsoft Excel – بثلاث طرق مختلفة.
- الطريقة الأولى لحساب الفائدة المركبة هي مضاعفة الرصيد الجديد لكل سنة في سعر الفائدة. لنفترض أنك قمت بإيداع 1000 دولار في حساب توفير بمعدل فائدة 5٪ يتراكم سنويًا، وتريد حساب الرصيد في خمس سنوات. في Microsoft Excel، أدخل “السنة” في الخلية A1 و “الرصيد” في الخلية B1. ثم أدخل السنوات من 0 إلى 5 في الخلايا من A2 إلى A7. رصيد السنة 0 هو 1000 دولار، لذا يمكنك إدخال “1000” في الخلية B2. بعد ذلك، أدخل “= B2 * 1.05” في الخلية B3. ثم أدخل “= B3 * 1.05” في الخلية B4 واستمر في القيام بذلك حتى تصل إلى الخلية B7. في الخلية B7، سيكون الحساب “= B6 * 1.05”. أخيرًا، القيمة المحسوبة في الخلية B7 سيكون 1,276.28 دولارًا ويمثل الرصيد في حساب التوفير بعد خمس سنوات. ولإيجاد قيمة الفائدة المركبة، اطرح 1،000 دولار من 1,276.28 دولار؛ وبذلك تكون قيمة الفائدة المركبة 276.28 دولارًا.
- الطريقة الثانية لحساب الفائدة المركبة هي استخدام صيغة ثابتة.
صيغة الفائدة المركبة هي (P*(1+i)^n) – P))، حيث P هو المبلغ الأساسي، و i معدل الفائدة السنوية، و n هو عدد الفترات. باستخدام نفس المعلومات أعلاه، أدخل “القيمة الأساسية” في الخلية A1 و 1000 في الخلية B1. بعد ذلك، أدخل “معدل الفائدة” في الخلية A2 و “.05” في الخلية B2. أدخل “الفترات المركبة” في الخلية A3 و “5” في الخلية B3.
يمكنك الآن حساب الفائدة المركبة في الخلية B4 عن طريق إدخال “= (B1 * (1 + B2) ^ B3) -B1″، مما يعطيك نفس الإجابة السابقة 276.28 دولارًا. - الطريقة الثالثة لحساب الفائدة المركبة هي إنشاء دالة ماكرو. ابدأ أولاً بتشغيل محرر فيجوال بيسيك Visual Basic، الموجود في علامة تبويب المطور. انقر فوق قائمة “إدراج”، وانقر فوق موديول (Module). ثم اكتب في السطر الأول:
“Function Compound_Interest (P As Double، i As Double، n As Double) As Double”
وفي السطر الثاني، اضغط على مفتاح tab واكتب:
“Compound_Interest = (P * (1 + i) ^ n) – P”.
في السطر الثالث من الموديول ، أدخل :
“End Function”.
اذا اتبعت الخطوات السابقة ستكون قد قمت بإنشاء دالة ماكرو لحساب معدل الفائدة المركبة. متابعا في نفس ورقة عمل اكسل أعلاه، أدخل “الفائدة المركبة” في الخلية A6 وأدخل
“= Compound_Interest (B1، B2، B3)”
سيمنحك هذا قيمة 276.28 دولارًا والتي تتوافق مع القيمتين الأوليين.
استخدام حاسبات أخرى
كما ذكرنا أعلاه، يوجد عدد من حاسبات الفائدة المركبة المجانية عبر الإنترنت، ويمكن للعديد من الآلات الحاسبة المحمولة تنفيذ هذه المهام أيضًا.
- حاسبة الفائدة المركبة المجانية المقدمة من خلال Financial-Calculators.com سهلة التشغيل وتوفر خيارات تردد مركبة من يوميًا إلى سنويًا. وتتضمن خيارًا لتحديد التركيب المستمر ويسمح أيضًا بإدخال تواريخ البدء والانتهاء الفعلية. بعد إدخال البيانات الحسابية اللازمة، تظهر النتائج الفائدة المكتسبة، والقيمة المستقبلية، ونسبة العائد السنوي (APY)، وهو مقياس يتضمن الفائدة المركبة والفائدة اليومية.
- يقدم موقع Investor.gov، وهو موقع إلكتروني تديره هيئة الأوراق المالية والبورصات الأمريكية (SEC)، حاسبة فائدة مركبة مجانية عبر الإنترنت. الحاسبة بسيطة إلى حد ما، لكنها تسمح بإدخال ودائع شهرية إضافية للمبلغ الأساسي، وهو أمر مفيد لحساب الأرباح حيث يتم إيداع مدخرات شهرية إضافية.
- وهناك حاسبة فائدة أخرى مجانية عبر الإنترنت مع بعض الميزات الإضافية على موقع TheCalculatorSite.com وتتيح هذه الآلة الحاسبة إجراء حسابات للعملات المختلفة، والقدرة على احتساب الإيداعات أو السحوبات الشهرية، وخيار الحصول على زيادات معدلة حسب التضخم على الودائع الشهرية أو السحوبات المحسوبة تلقائيًا أيضًا.
تكرار التركيب
يمكن مضاعفة الفائدة على أي جدول تكرار معين، من يومي إلى سنوي. وهناك جداول تكرار تركيب قياسية يتم استخدامها عادة للأدوات المالية.
جدول تكرار التركيب المستخدم بشكل شائع لحساب التوفير في البنك هو يومي. بالنسبة لشهادات الإيداع، تكون جداول تكرار التركيب النموذجية يومية أو شهرية أو نصف سنوية؛ بالنسبة لحسابات سوق المال، غالبًا ما يكون ذلك يوميًا. بالنسبة لقروض الرهن العقاري، أو قروض ملكية المنازل، أو قروض الأعمال الشخصية، أو حسابات بطاقات الائتمان، فإن الجدول الزمني المركب الأكثر شيوعًا هو الشهري. يمكن أن تكون هناك أيضًا اختلافات في الإطار الزمني الذي يتم فيه قيد الفائدة المستحقة بالفعل في الرصيد الحالي. قد تتضاعف الفائدة على الحساب يوميًا ولكن يتم إيداعها شهريًا فقط. وفقط عندما يتم إضافة الفائدة فعليًا أو إضافتها إلى الرصيد الحالي، تبدأ في كسب فائدة إضافية في الحساب.
تقدم بعض البنوك أيضًا شيئًا يسمى الفائدة المركبة المستمرة، والتي تضيف فائدة إلى رأس المال في كل لحظة ممكنة. لأغراض عملية، لا تتراكم أكثر بكثير من الفائدة المركبة اليومية إلا إذا كنت ترغب في استثمار الأموال وإخراجها في نفس اليوم.
تضاعف الفائدة بشكل متكرر مفيد للمستثمر أو الدائن. بالنسبة للمقترض، فإن العكس هو الصحيح.
اعتبار القيمة الزمنية لأموال
يعد فهم القيمة الزمنية للنقود والنمو المتسارع الناتج عن التركيب أمرًا ضروريًا للمستثمرين الذين يتطلعون إلى تحسين الدخل وتخصيص الثروة.
صيغة الحصول على القيمة المستقبلية (FV) والقيمة الحالية (PV) هي كما يلي:
القيمة المستقبلية= القيمة الحالية *((1+ نسبة الفائدة)^عدد الفترات)
أو FV = PV (1 +i)n
القيمة الحالية= القيمة المستقبلية / ((1+ نسبة الفائدة)^عدد الفترات)
PV = FV / (1 + i) )n
على سبيل المثال، القيمة المستقبلية لبغ 10,000 دولار مركبة بنسبة 5٪ سنويًا لمدة ثلاث سنوات:
=$10,000 (1+0.05)3
=$10,000 (1.157625)
=$11,576.25
ويمكن حساب القيمة الحالية لـ 11,576.25 دولار مخصومة بنسبة 5٪ لمدة ثلاث سنوات:
=$11,576.25/ (1+0.05)3
=$11,576.25/1.157625
=$10,000
ويكون مقلوب 1.157625، والذي يساوي 0.8638376، هو عامل الخصم في هذه الحالة.
اعتبارات القاعدة 72
تحسب ما يسمى بقاعدة 72 الوقت التقريبي الذي سيتضاعف فيه الاستثمار بمعدل معين من العائد أو الفائدة “i”، ويتم تقديمه بواسطة (72\الفائدة). ويمكن استخدامه فقط للتركيب السنوي.
على سبيل المثال، سيتضاعف استثمار معدل عائده السنوي 6٪ خلال 12 عامًا.
وسيتضاعف استثمار يبلغ معدل عائده السنوي 8٪ سيتضاعف في غضون تسع سنوات.